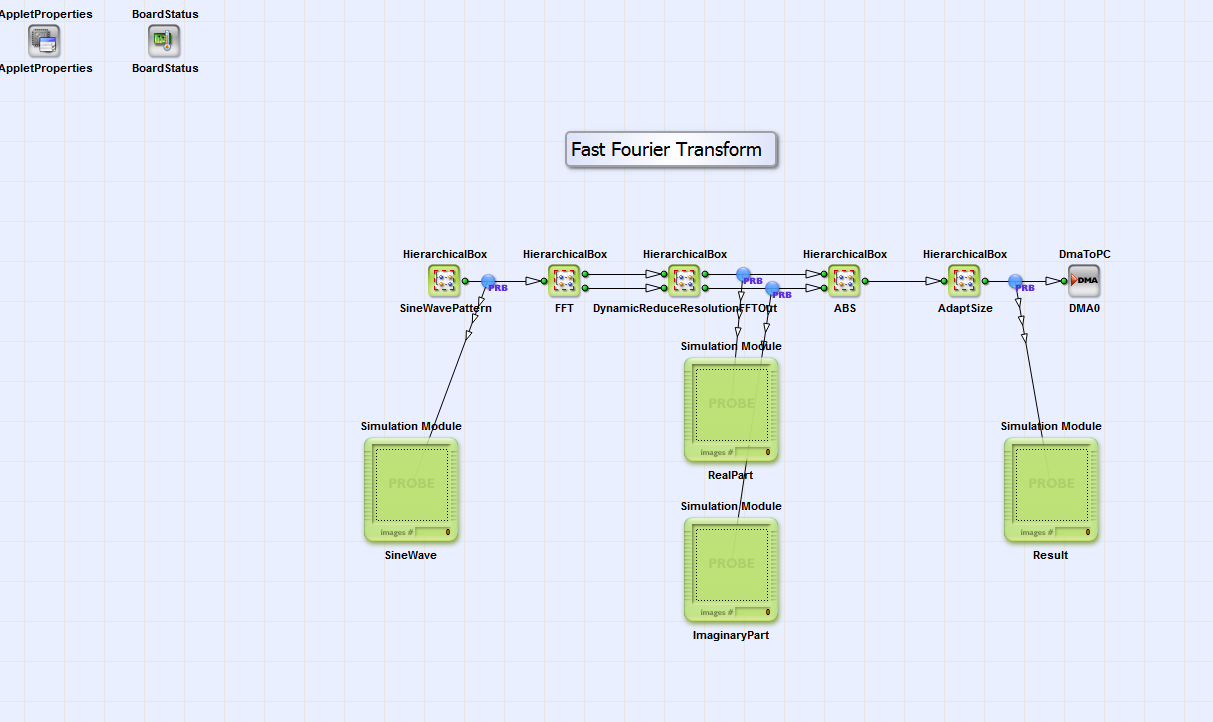
| Brief Description | |
|---|---|
|
File: \examples\Processing\FastFourierTransform\mE5-MA-VCL\fft.va File: \examples\Processing\FastFourierTransform\mE5-VD8-CL\fft.va File: \examples\Processing\FastFourierTransform\iF-CXP12-Q\fft.va |
 |
|
Default Platform: mE5-MA-VCL, mE5-VD8-CL and iF-CXP12-Q |
|
|
Short Description Shows the usage of operator FFT. The applet generates a sine pattern and performs the FFT. The results show the frequency part. Use the VisualApplets simulation. |
|
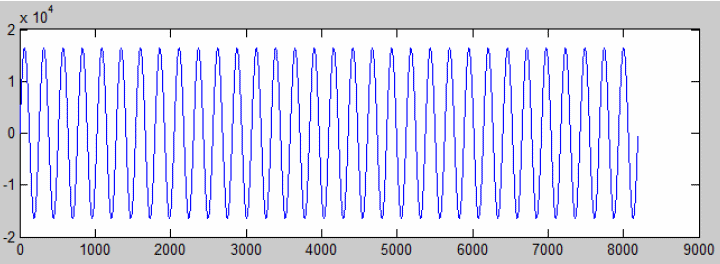
The provided example will demonstrate the use of the FFT. In the example, a simple sine wave with period 256 and magnitude ± 16384 and an image width of 2048 pixels (or 4096 pixels for mE5-VD8-CL) is generated.
The VisualApplets implementation is very simple. A sine wave input is forwarded to the FFT operator. The resulting real and imaginary part are squared and added. So the output is the squared absolute value. The result shows the expected peak at x = 8 (or 32 mE5-VD8-CL) i.e. a period of 2048 / 8 (8192/32 for mE5-VD8-CL)= 256. A comparison with Matlab FFT calculation shows a very similar result in the same accuracy range. H-Box "DynamicReduceResolutionFFTOut" is used to shift results and reduce their resolution. This is not required for the given sine wave but is an option for other requirements.
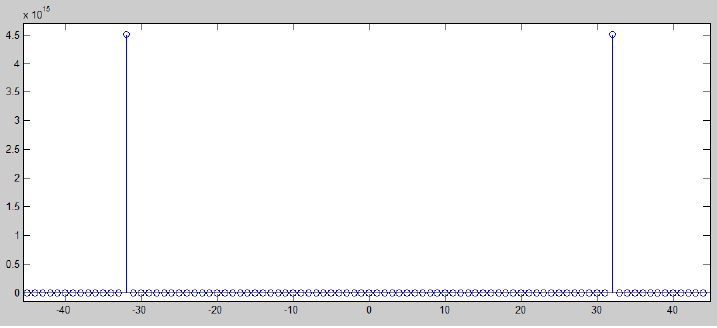
Figure 318. FFT Result for mE5-VD8-CL. At position 32 the real part value is -43 and imaginary part is -67108738.

 Prev
Prev